双曲线的顶点和焦点有什么区别？（零的焦点剧情介绍）

双曲线的顶点和焦点有什么区别？

双曲线的顶点与焦点是不同的：

(1)定义不同：双曲线上的点到定点的距离差的绝对值是常数，其中的定点叫焦点。顶点是双曲线与对称轴的交点。

(2)位置不同：顶点在双曲线上，焦点不在双曲线上。

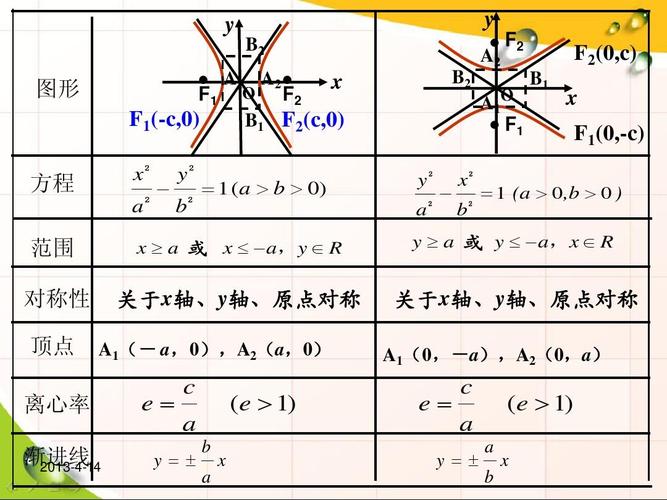
(3)坐标不同：以x^2/a^2-y^2/b^2＝1为例，顶点坐标是(-a，0)(a，0)，焦点坐标是(-c，0)(c，0)。

双曲线的定点不会是焦点的，如果焦点在x轴上，右顶点（a，0），右焦点（c，0），c大于a，两点不会重合的。

双曲线的焦点坐标？

　　焦点在x轴(-c，0)、(c，0);焦点在y轴：(0，-c)、(0，c)。双曲线有两个焦点，焦点的横(纵)坐标满足c²=a²+b²。平面内，到给定一点及一直线的距离之比为常数e((e>1)，即为双曲线的离心率)的点的轨迹称为双曲线。定点叫双曲线的焦点。

　　1、双曲线的焦点算法

　　(1)化成标准方程：x²/a²-y²/b²=1(a>0，b>0)

　　(2)根据关系：c²=a²+b²，求出c。

　　(3)表示焦点坐标(-c，0)(c，0)。

椭圆上哪一点到焦点的距离最小,为什么?求证明？

可设椭圆方程为(x²/a²)+(y²/b²)=1 (a＞b＞0)两个焦点F1(-c,0),F2(c,0)长轴的两个端点A1(-a,0),A2(a,0)因点P在椭圆上,故可设P(acost,bsint),t∈R.由两点间距离公式可得|PF1|²=(acost+c)²+(bsint)²=a²cos²t+2accost+c²+b²sin²t=(a²-b²)cos²t+2accost+c²+b²=c²cos²t+2accost+a²=(a+ccost)²由-1≤cost≤1 且a＞c＞0可知0＜a-c≤a+ccost≤a+c∴|PF1|=a+ccost.∴| PF1|min=a-c.此时,cost=-1,sint=0,P(-a,0)又|PF1|+|PF2|=2a.∴当|PF1|min=a-c时,|PF2|max=a+c,此时点P在长轴的一个端点上.

两个焦点的距离公式？

焦距计算公式：

f=v× D/V---(1) f=h× D/H---(2)

f: 镜头的焦距长度

V：拍摄对象的纵向尺寸

H：拍摄对象的横向尺寸

一、双曲线的相关概念

焦点：双曲线有两个焦点。焦点的横（纵）坐标满足c²=a²+b²。

离心率：给定点与给定直线的距离之比，称为该双曲线的离心率。离心率e=c/a

顶点：双曲线和它的对称轴有两个交点,它们叫做双曲线的顶点。

实轴：两顶点之间的距离称为双曲线的实轴,实轴长的一半称为实半轴。

虚轴：在标准方程中令x=0,得y²=-b²，该方程无实根，为便于作图，在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴.

渐近线：双曲线有两条渐近线。渐近线和双曲线不相交。

焦点在x轴的渐近线：y=±b/a x

焦点在y轴的渐近线：y=±a/b x

到此，以上就是小编对于零的焦点剧情解析的问题就介绍到这了，希望介绍的4点解答对大家有用。